↜ Back to index Introduction to Numerical Analysis 1

Part b—Lecture 7

Report 2 is assigned. Submit the solutions by August 6 (Friday) to LMS.

We talk about a notion of energy in the wave equation and its conservation.

Mechanical energy in the wave equation

The wave equation is a model a vibration of various physical systems. Such a system has a mechanical energy that is conserved (it does not change with time) in the ideal case¹. It is usually the sum of the kinetic energy and the elastic energy. For the one-dimensional wave equation on space domain (0, 1), the total energy of the system at time t \geq 0 is defined as E(t) := \frac 12\int_0^1\big[(u_t(x,t))^2 + (u_x(x,t))^2\big] \;dx. Note carefully how the integral is computed: t is fixed, and the function (u_t)^2 + (u_x)^2 is integrated in x only.

To see that E(t) is constant in time, we compute its derivative, assuming that u is a solution of the wave equation for x \in (0, 1), t > 0: \begin{aligned} \frac{d {E}}{d {t}}(t) &= \frac12 \int_0^1 \frac{\partial {}}{\partial {t}} \big[(u_t)^2 + (u_x)^2\big] \;dx\\ &= \frac12 \int_0^1 \big[2 u_t u_{tt} + 2 u_x u_{xt}\big] \;dx\\ &= \int_0^1 \big[u_t u_{tt} + u_x u_{xt}\big] \;dx. \end{aligned} We now use that \frac{\partial^2 u}{\partial x \partial t} = \frac{\partial^2 u}{\partial t \partial x} so that u_{xt} = u_{tx}= \frac{\partial {u_t}}{\partial {x}}. We can now use integration by parts on the second integrand: \int_0^1 u_x \frac{\partial {u_t}}{\partial {x}} \;dx= [u_x u_t]_0^1 - \int_0^1 \underbrace{\frac{\partial {u_x}}{\partial {x}}}_{= u_{xx}} u_t. Putting it back, we have \frac{d {E}}{d {t}}(t) = \int_0^1 \big[u_t u_{tt} - u_t u_{xx}\big] \;dx+ [u_x u_t]_0^1. But since u solves the wave equation u_{tt} = u_{xx}, we see that the integral is 0 and so \frac{d {E}}{d {t}}(t) = [u_x u_t]_0^1 = u_x(1,t) u_t(1, t) - u_x(0, t) u_t(1,t). We can now conclude that the derivative is zero for the following boundary conditions:

Dirichlet: u(0, t) = a, u(1, t) = b so that u_t(0, t) = 0 = u_t(1,t).
Neumann with zero: u_x(0, t) = 0 = u_x(1, t).

Or we can have Dirichlet on one side and Neumann with zero on the other. In all these situations we get \frac{d {E}}{d {t}}(t) = 0 and therefore E(t) = E(0) \qquad t \geq 0. Note that E(0) is given by the initial data: E(0) = \frac 12\int_0^1\big[(u_{0,t})^2 + (u_{0,x})^2\big] \;dx.

Uniqueness of solutions using the conservation of energy

The fact that E(t) is constant in time is very useful to study the solutions of the wave equation. For example, we can prove the uniqueness of solutions:

Theorem. Suppose that u_1 and u_2 are two smooth solutions of the wave equation for x \in (0,1) and t > 0 with the same initial data u_0 and v_0 and the same Dirichlet boundary condition. Then u_1 = u_2 \qquad x \in (0,1), t > 0. That is, this problem has only one solution.

Proof. Since u_1 and u_2 are solutions, u := u_1 - u_2 is also a solution but with initial data u(x, 0) = 0 and u_t(x, 0) = 0, and with zero Dirichlet data. Therefore the energy E(0) = 0 and by the energy conservation E(t) = E(0) = 0 \qquad t > 0. But this means that u_t = 0 = u_x for all x \in (0,1), t > 0 and so u is a constant function. Since u = 0 at t = 0 or at x = 0 or at x = 1, u \equiv 0 and so u_1 \equiv u_2.

Report 2

Submit the solutions by August 6 (Friday) to LMS. All subproblems are worth 10 points, except 3-3. that is worth 20 points.

Exercise 1.

Write a Fortran program that solves the wave equation on x \in (0, 1), t \in (0, 2] with initial data u_0(x) = \sin(\pi x) and v_0(x) = \pi \sin(3 \pi x) with Dirichlet boundary condition u(0, t) = u(1, t) = 0, and outputs t_n and the value of the discrete energy E_n (see below) at each time step n = 1, \ldots, n_{\rm max} - 1. Here n_{\rm max} = 2 / \tau.

To compute the discrete energy, use the following approximation: E_n := \frac h2 \sum_{k = 1}^{M-1} \left[\left(\frac{|u_{n+1, k} - u_{n-1, k}|}{2\tau}\right)^2 + a_k\left(\frac{|u_{n, k-1} - u_{n, k+1}|}{2h}\right)^2\right], where a_1 = a_{M-1} = \frac 32 and a_k = 1 for k = 2, \ldots, M-2.

For example, for M = 10, h = 1/M, \tau = h the output of my program is:

  0.100000001       4.27265549    
  0.200000003       4.20330620    
  0.300000012       4.73033428    
  0.400000006       4.81650496    
  0.500000000       4.53170061    
  0.600000024       4.66098547    
  0.699999988       4.88585234    
  0.800000012       4.86209774    
  0.900000036       4.93144560    
   1.00000000       4.80909491    
   1.10000002       4.27265406    
   1.20000005       4.20330572    
   1.30000007       4.73033333    
   1.39999998       4.81650400    
   1.50000000       4.53170013    
   1.60000002       4.66098499    
   1.70000005       4.88585281    
   1.80000007       4.86209822    
   1.89999998       4.93144560

Submit the program that does the computation with M = 10, h = 1/M, \tau = h. 問1
Plot the energy as a function of t_n using gnuplot with M = 10, h = 1/M, \tau = h. Submit the plot with your student ID as the title. 問2
Plot the energy as a function of t_n using gnuplot with M = 512, h = 1/M, \tau = h. Use with lines in gnuplot. Submit the plot with your student ID as the title. 問3

Exercise 2.

Write a Fortran program that solves the wave equation on x \in (0, 1), t \in (0, 2] with initial data u_0(x) = \cos(2 \pi x) and v_0(x) = \pi \sin(3 \pi x) with Neumann boundary condition u_x(0, t) = u_x(1, t) = 0, and outputs t_n and the value of the discrete energy E_n (see below) at each time step n = 1, \ldots, n_{\rm max} - 1.

To compute the discrete energy, use the following approximation: E_n := \frac h2 \sum_{k = 0}^M b_k\left(\frac{|u_{n+1, k} - u_{n-1, k}|}{2\tau}\right)^2 + \frac h2\sum_{k=1}^{M-1}\left(\frac{|u_{n, k-1} - u_{n, k+1}|}{2h}\right)^2, where b_0 = b_M = \frac 12 and b_k = 1 for k = 1, \ldots, M-1.

For example, for M = 10, h = 1/M, \tau = h the output of my program is:

  0.100000001       11.1046886    
  0.200000003       11.1046877    
  0.300000012       11.1046877    
  0.400000006       11.1046877    
  0.500000000       11.1046877    
  0.600000024       11.1046877    
  0.699999988       11.1046867    
  0.800000012       11.1046867    
  0.900000036       11.1046877    
   1.00000000       11.1046877    
   1.10000002       11.1046886    
   1.20000005       11.1046886    
   1.30000007       11.1046867    
   1.39999998       11.1046877    
   1.50000000       11.1046877    
   1.60000002       11.1046877    
   1.70000005       11.1046877    
   1.80000007       11.1046886    
   1.89999998       11.1046877

Submit the program that does the computation with M = 10, h = 1/M, \tau = h. 問4
Plot the energy as a function of t_n using gnuplot with M = 10, h = 1/M, \tau = h. Submit the plot with your student ID as the title. 問5
Plot the energy as a function of t_n using gnuplot with M = 512, h = 1/M, \tau = h. Use with lines in gnuplot. Submit the plot with your student ID as the title. 問6

Exercise 3. (This is Exercise 3 from Lecture 6)

Implement a Fortran program that solves the wave equation with the initial data \begin{aligned} u_0(x) &= f(8 x - 2), &&x \in [0, 1]\\ v_0(x) &= 8f'(8 x - 2), &&x \in [0, 1], \end{aligned} where f(s) := \begin{cases} \exp{\frac 1{s^2 - 1}} & |s| < 1,\\ 0, & \text{otherwise}. \end{cases} and the Dirichlet boundary condition u(0, t) = 0 at x = 0 and the Neumann boundary condition u_x(1, t) = 0.

Plot the numerical solution with M = 64, h = 1/ M, \tau = h on the time interval t \in [0, 2] using the usual gnuplot’s splot … with lines. Submit the plot with your student ID as the title. 問7
Plot the numerical solution with the parameters in 1. at time steps n = 14, n =16 and n = 25 in one plot. Submit the plot with your student ID as the title. 問8
Submit the Fortran program that you used to produce the data for 1. 問9

Example solutions

1-2

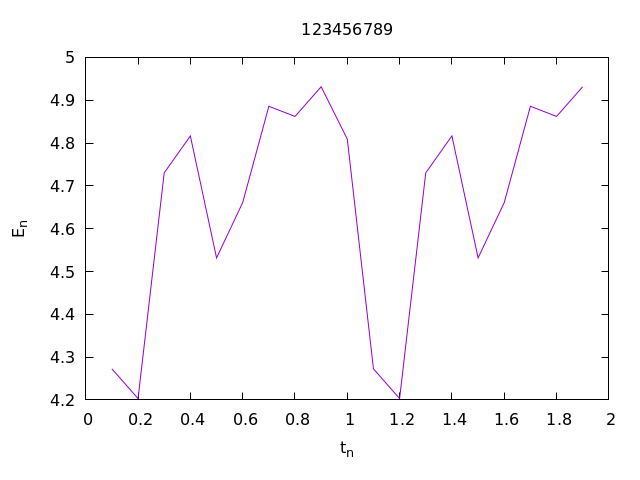
2-2

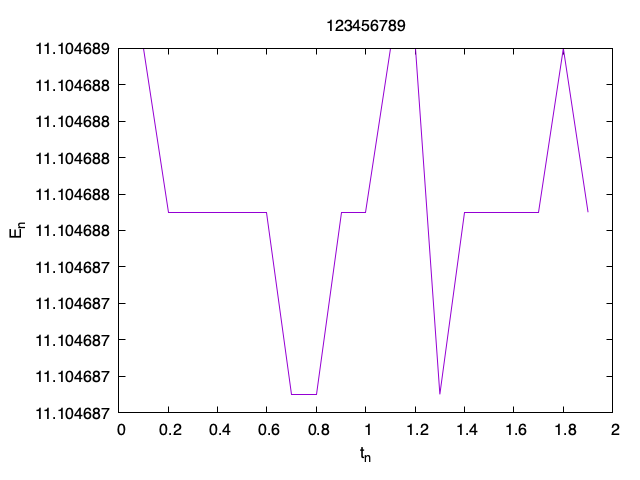
It is slowly converted to heat in real systems.↩︎